How To Find An Eigenvector: The Definitive Step-by-Step Guide for Scientists and Statisticians

Unlocking the hidden structure of matrices through eigenvectors is a cornerstone of linear algebra, offering profound insights across physics, engineering, machine learning, and data science. For those navigating complex systems, understanding how to locate eigenvectors transforms abstract mathematical concepts into practical tools for analysis and prediction. Eigenvectors reveal directions in vector spaces that remain invariant under specific linear transformations—representing fundamental modes of change—making their identification both mathematically powerful and computationally essential.

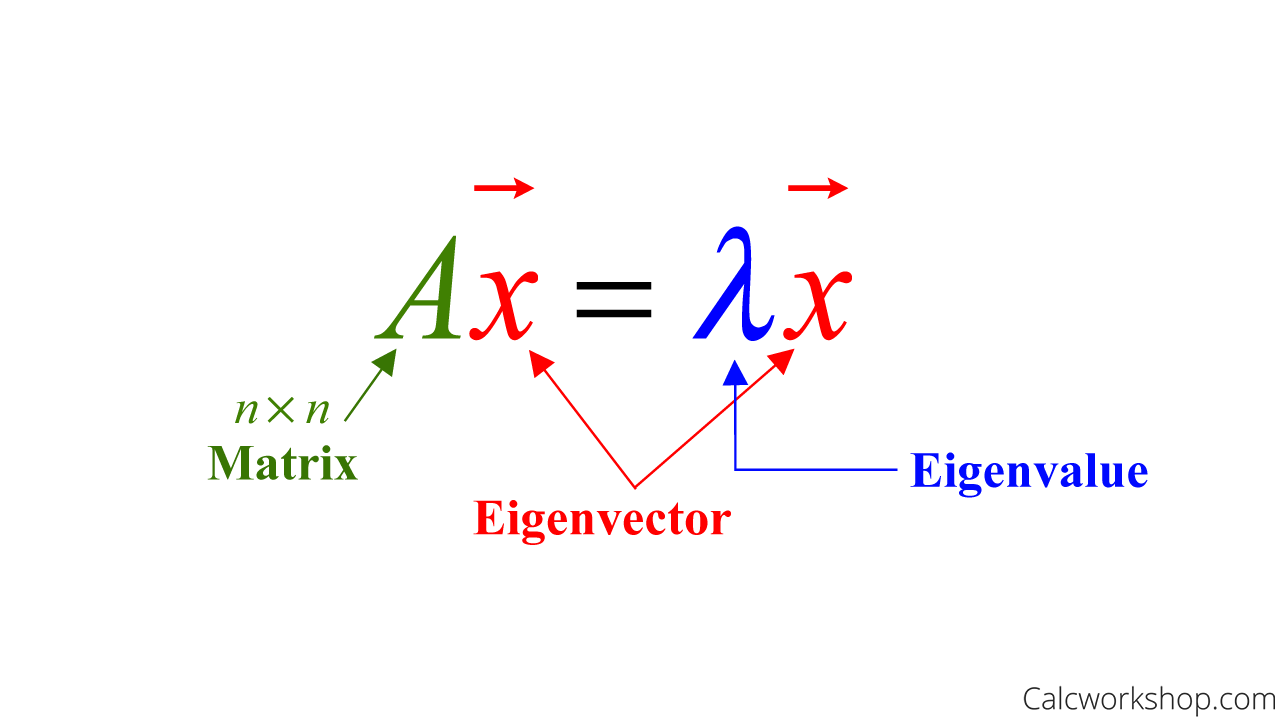
At its core, an eigenvector of a square matrix represents a non-zero vector that, when transformed by the matrix, only scales—never rotates or changes direction. Mathematically, if \( A \) is a square matrix and \( v \) a non-zero vector, then \( v \) is an eigenvector if A v = λ v, where \( λ \) is the associated eigenvalue. This multiplicative relationship reveals stability and scaling characteristics of linear systems, critical in modeling everything from quantum states to economic networks.

> The process of finding eigenvectors unfolds in a structured sequence, beginning with foundational requirements and culminating in precise computation.

To identify eigenvectors reliably, one must first satisfy key prerequisites that anchor the method in mathematical rigor.

Key Prerequisites: Matrix Properties and Condition Checks

Not all matrices yield meaningful eigenvectors. Before proceeding, verify that the matrix \( A \) is square (equal number of rows and columns), as eigenvalues and eigenvectors are defined exclusively for square matrices.

For small systems, this is straightforward; for larger ones, using determinants and characteristic polynomials becomes essential. Next, confirm that \( A \) is diagonalizable—meaning it possesses a full set of linearly independent eigenvectors. A matrix fails to be diagonalizable if it contains defective eigenvalues (those with insufficient eigenvectors to span the space), such as repeated eigenvalues without adequate geometric multiplicity.

"A matrix must balance algebraic and geometric multiplicities to guarantee diagonalizability," notes linear algebra expert Dr. Elena Torres. This condition ensures that each eigenvector contributes independently to decomposing the matrix.

Step 1: Derive the Characteristic Polynomial

The first computational step involves constructing the characteristic polynomial, defined by the determinant of \( (A - λI) \), where \( I \) is the identity matrix and \( λ \) represents eigenvalues. For a \( 3 \times 3 \) matrix: \[ \det(A - λI) = -λ^3 + \text{tr}(A)λ^2 - ( \text{sum of principal minors )}λ + \det(A) \] This cubic equation yields eigenvalues as its roots—each candidate for scalar multiplier in the eigenvector equation. For larger matrices, numerical methods or software tools streamline this process, but symbolic computation remains vital for accuracy.

While the characteristic polynomial identifies eigenvalues, it offers no vector—the next phase transforms roots into directional insight.

< Once eigenvalues are known, solving \( (A - λI)v = 0 \) yields eigenvectors for each eigenvalue \( λ \). This homogeneous system reveals solutions by expressing the matrix equation as a linear system. For each \( λ \), rows of \( A - λI \) vanish, reducing the space to nontrivial solutions for \( v \).

Consider a \( 3 \times 3 \) matrix: \[ A - λI = \begin{bmatrix} a-λ & b & c \\ d & e-λ & f \\ g & h & i-λ \end{bmatrix} \] Row reduction isolates free variables, which parameterize eigenvectors. For each eigenvalue, eliminate variables to express basis vectors. For example, in a 3×3 matrix with eigenvalue \( λ = 2 \), after row reduction, if pivot variables are expressed in terms of a free variable \( t \), the eigenvector takes the form \( v = t \begin{bmatrix} x \\ y \\ t \end{bmatrix} \)—a directional marker across the system’s invariant subspace.

The choice of parameter matters. Repeated trials with different free variables may yield scalar multiples, reinforcing that eigenvectors exist along unique directions rather than specific vectors.