How to Find the Volume of a Rectangle: The Essential Step-by-Step Guide

Unlocking the secret to calculating the volume of a rectangle may seem deceptively simple—but mastering this foundational skill is crucial across architecture, engineering, and everyday spatial reasoning. Whether you're designing a room, shipping goods, or solving inventory logistics, knowing how to find the volume of a rectangular prism enables precise measurements and informed decisions. This article reveals a clear, reliable method to compute rectangular volume with confidence—no guesswork, no confusion.

At its core, the volume of a rectangle is a three-dimensional measure expressing the space an object occupies.

For a perfect rectangular prism, volume is determined by a straightforward multiplication: length multiplied by width multiplied by height. But how do professionals and learners alike perform this calculation correctly? The process follows a logical sequence rooted in geometry’s fundamental principles.

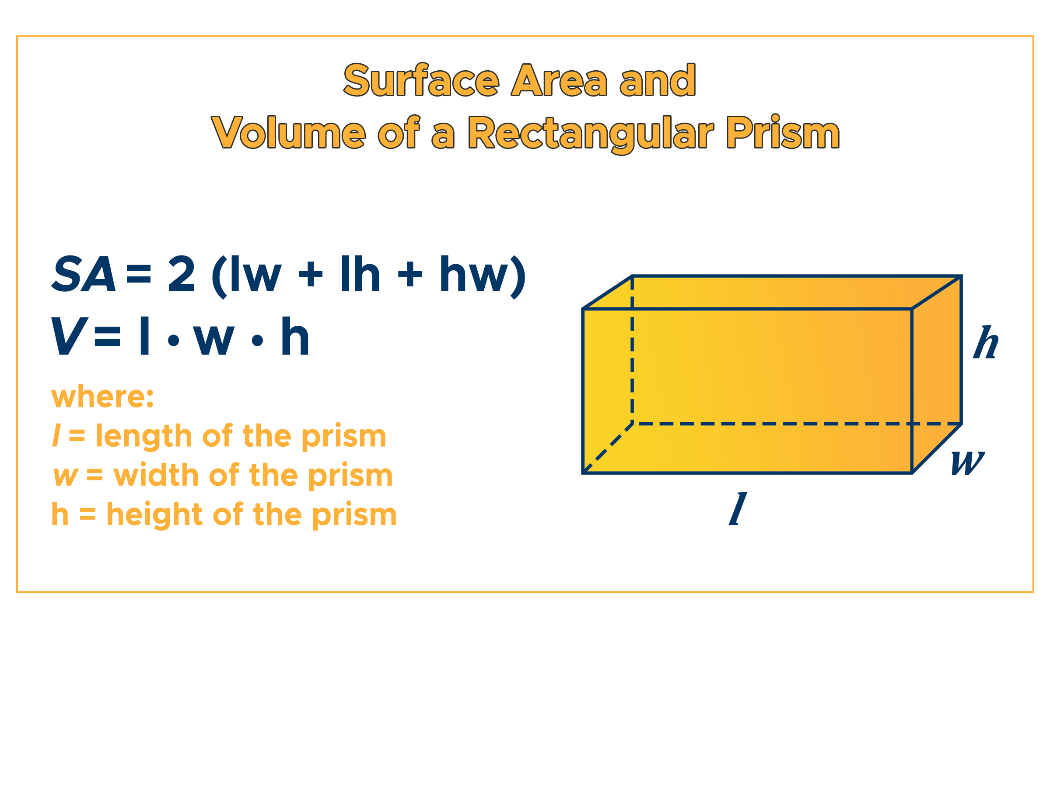
Understanding the Rectangular Volume Formula

The volume (V) of any rectangular solid is calculated using the formula:

V = l × w × h

where:
• V = Volume in cubic units (e.g., cubic meters, cubic feet)
• l = Length (longest side, in chosen units)
• w = Width (shortest side)
• h = Height (depth or vertical dimension)

This formula stems from the definition of volume as the area of the base (length × width) extended into thickness.

Only dimensions measured in the same units yield accurate results. For example, recording length in feet, width in feet, and height in feet produces volume in cubic feet—ensuring dimensional consistency.

Step-by-Step: How to Find Volume of a Rectangle

Success hinges on precision in each measurement and calculation step. Follow this proven sequence:

1. Measure with Accuracy: Use calibrated tools such as laser measures or digital calipers to record dimensions.

   Minor errors compound quickly—treat each measurement with care, capturing multiple readings if needed to validate consistency.

2. Identify Correct Dimensions: Clearly define what represents length, width, and height based on context. In construction, for instance, ‘length’ may refer to the building’s longest side parallel to the porch, while ‘height’ aligns with vertical rise from foundation to ceiling.
3. Apply the Formula: Multiply length by width to determine the area of the base. Then multiply the result by height to extend this two-dimensional space into full volume.
4. Verify Units: Ensure all measurements use the same unit system (e.g., meters, feet).

   Convert if necessary—1 foot equals 0.3048 meters—to prevent dimensional mismatch.

5. Execute the Math: Use a calculator or digital software for efficiency, especially in large-scale applications. Double-check arithmetic operations to maintain accuracy.

For example, calculating the storage volume of a warehouse rack: if a shelf unit is 4 meters long, 2 meters wide, and 3 meters tall, the volume is 4 × 2 × 3 = 24 cubic meters. This space supports exactly 24,000 liters—critical data for logistics planning.

Common Pitfalls and How to Avoid Them

Even seasoned practitioners can stumble if they overlook key details.

Avoid these frequent errors:

• Mixing Up Dimensions: Confusing length with height can distort results. Always map each measurement to its geometric position—use visual aids or diagrams if needed.
• Neglecting Unit Consistency: Mixing meters and inches yields nonsensical output. Keep all units aligned before multiplication.
• Trailing Zeros or Rounding Errors: Rounding intermediate steps too early introduces small inaccuracies.

  Retain full precision until final reporting.

• Assuming Rectangularity: Volume is accurate only for true rectangular shapes. Irregular solids require integration or approximation methods.

Experts stress maintaining geometric clarity: “Always define axes before calculation—this prevents ambiguity and ensures repeatable, trustworthy results,” notes Dr. Elena Torres, structural analyst at the Global Construction Institute.

Applications Beyond the Classroom

The volume of a rectangle permeates real-world scenarios, from construction timbers to packaging design.

Consider these practical use cases:

• Construction and Civil Engineering: Calculating concrete volumes for slabs, foundations, or retaining walls demands precise rectangular calculations to prevent material waste and ensure structural integrity.
• Packaging and Logistics: Companies optimize box dimensions to minimize shipping costs while maximizing internal space—efficiency hinges on accurate volume estimation.
• Interior Design and Renovation: Homeowners and designers use volume to assess room capacity, furniture placement, and climate control needs—critical for comfort and functionality.
• Agriculture and Storage: From grain silos to walk-in freezers, maintaining proper volume supports inventory management and resource planning.

Each application relies on applying the volume formula with contextual precision—transforming abstract math into tangible value.

In essence, mastering how to find the volume of a rectangle is about more than formulas—it’s about cultivating spatial accuracy that bridges theoretical knowledge and real-world execution. The process is direct: measure carefully, apply the product of length, width, and height, ensure consistent units, and verify results. Repeat this sequence, and errors shrink.

Confidence grows. And so does the power