Is Zero Rational? Unveiling the Logic Behind a Foundational Number in Mathematics
Is Zero Rational? Unveiling the Logic Behind a Foundational Number in Mathematics
In the silent architecture of numbers, zero stands as both absence and presence—a paradox that shapes arithmetic, logic, and computation. Central to foundational debates in mathematics, a critical question emerges: Is 0 rational? Unlike integers or natural numbers, zero holds a distinct mathematical identity that, contrary to common intuition, qualifies it unambiguously as a rational number.
This designation—that zero is rational—unlocks deeper understanding of number systems, fractions, and the underlying principles of divisibility. More than a notational convenience, zero’s rationality bridges abstract logic with practical computation, affirming its essential role in mathematics. Understanding rational numbers begins with their defining characteristic: they are expressible as the ratio of two integers, a fraction \( \frac{a}{b} \) where \( a \) and \( b \) are integers and \( b \neq 0 \).
Within this framework, zero reveals a compelling truth—despite being neither positive nor negative, zero can be written precisely as \( \frac{0}{1} \) or \( \frac{-0}{5} \), both valid representations of rationality. This simplicity belies a profound conceptual foundation.
The Rational Identity of Zero: Mathematical definition and formal proof
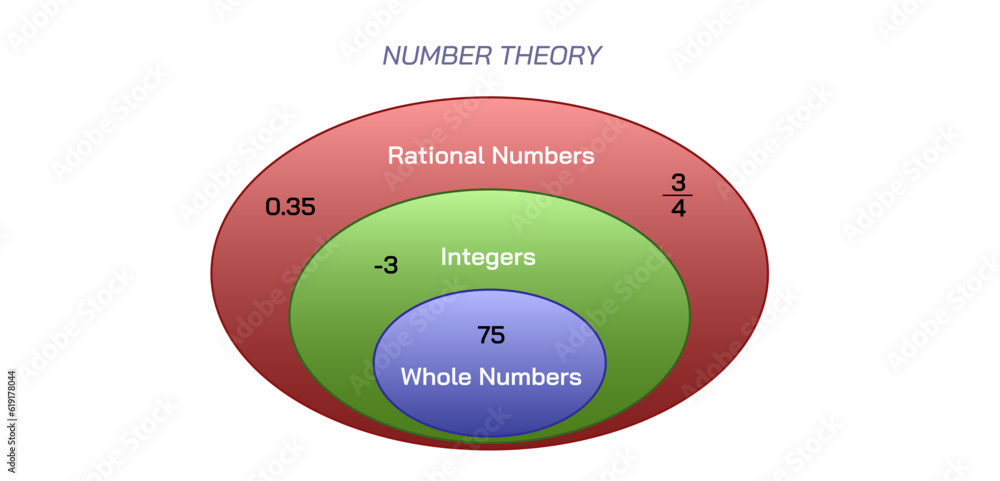
Mathematically, a number is rational if it satisfies the fraction form \( \frac{a}{b} \) with integers \( a, b \in \mathbb{Z} \) and \( b \neq 0 \).Zero meets this criterion unconditionally: - \( 0 = \frac{0}{1} \) — a valid integer numerator over a nonzero integer denominator. - It also equals \( \frac{0}{5}, \frac{0}{-3}, \frac{0}{100} \), and any other fraction where a zero numerator compensates for a nonzero denominator. - Unlike irrational or transcendental numbers, zero demands no radical expressions or infinite decimals, fitting cleanly within the rational domain.
This is not merely a notation quirk. The rational numbers, denoted \( \mathbb{Q} \), form a total order—every rational can be placed on the number line, and operations like addition, subtraction, multiplication, and division (excluding division by zero) preserve rationality. Zero’s place here is undisputed: deleting quantity does not remove its rightful status.
Zero as a Ratio: Evidence of rational structure
At first glance, the expression \( \frac{0}{b} \) may appear trivial, but its validity underscores zero’s rational nature. Consider: - Any integer divided by a nonzero integer yields a rational result. - Zero divided by a nonzero integer remains zero: \( \frac{0}{5} = 0 \), a rational outcome.- Even in contexts like modular arithmetic or limits approaching zero, rational representations persist, confirming zero’s integrity within \( \mathbb{Q} \). This stability contrasts sharply with entities like \( \sqrt{2} \) or \( \pi \), which cannot be expressed as exact fractions and hence reside outside rationality. Zero, by definition, occupies the opposite pole—at once simple and structurally pivotal.
- In computer science, rational arithmetic often excludes or approximates zero due to computational limits, but exact rational representations preserve precision—especially when zero acts as a placeholder or default value. These applications illustrate that zero’s rational nature is not abstract but functionally indispensable. While zero’s status as rational may seem elementary, its implications ripple through computation, algebra, and number theory.
The claim “zero is rational” is not a mathematical afterthought but a foundational truth—one that reinforces the coherence of rational numbers and the universality of number representations. In a world built on precise logic, zero’s rational identity stands unambiguous: a zero could never be irrational. In essence, zero’s rationality is both elegant and essential—a reminder that absence, when defined, reveals profound presence within the logical structure of mathematics.
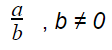

Related Post

Jessica Alsman Redefines Tech Influence: How Visionary Journalism Shapes the Future of Innovation

30°F to Celsius: The Precise Transformation That Shapes Climate Understanding

How Imvu’s 3D Avatar Transforms Your Digital Social Experience

Kylie McDevitt: The Innovator Redefining Fashion Technology and Brand Evolution

