Mastering Apex Algebra 1: Answers That Decode Success
Mastering Apex Algebra 1: Answers That Decode Success
Success in Apex Algebra 1 hinges on mastering its core concepts, understanding its unique problem-solving framework, and leveraging reliable, insightful resources. In a course designed to build algebraic fluency from foundational equations to real-world applications, learners face complex expressions, nonlinear relationships, and abstract reasoning. Answering these challenges effectively requires more than rote memorization—it demands strategic knowledge, structured practice, and access to clear, accurate explanations.
This article provides a definitive guide to key answers, critical strategies, and practical insights from Apex Algebra 1, empowering students and educators to transform confusion into confidence.
Decoding the Algebraic Mindset: What Apex Algebra 1 Demands
At its core, the curriculum emphasizes several pillars: - **Expressive Proficiency**: Writing equations and inequalities with precision, translating word problems into algebraic language, and working seamlessly with functions.
- **Logical Reasoning**: Applying deductive reasoning to validate solutions, analyzing graphs for behavior patterns, and identifying relationships between variables. - **Adaptive Application**: Using algebra to model real-world scenarios—from financial planning to scientific experimentation—requiring both abstract thinking and practical judgment.
< obligations, Apex Algebra 1 success depends on students’ ability to internalize core principles. For instance, distinguishing between proportional and non-proportional relationships is not just academic—it informs modeling decisions in economics and engineering.As one former teacher noted, “Algebra becomes powerful only when students see it not as formulas, but as a language of change.”
Key Answer Strategies for Algebraic Mastery
Effective problem-solving in Apex Algebra 1 goes beyond finding the “right” answer; it requires systematic deconstruction, verification, and connection-building. The process often unfolds in distinct, repeatable stages that cultivate clarity and accuracy.
Step 1: Understand the Problem Deeply Before reaching for a calculator or recalling rules, students must parse every component. This involves: - Identifying unknowns and assigning variables strategically.- Translating verbal or graphical statements into equations. - Recognizing constraints (e.g., domain restrictions, real-world limitations). - Highlighting key phrases like “rate,” “total,” or “increase” that signal mathematical operations.
Step 2: Apply Structured Problem-Solving Frameworks Apex Algebra 1 thrives on methodical strategies: - **Substitution**: Breaking complex expressions into manageable parts by replacing variables with known values. - **Graphical Interpretation**: Using coordinate geometry to visualize functions and relationships. - **Algebraic Manipulation**: Applying properties (commutative, distributive) and operations (addition, factoring) to isolate variables.
- **Cross-Verification**: Substituting solutions back into original equations to confirm validity—a critical safeguard against arithmetic errors. Step 3: Connect to Real-World Contexts One of the course’s most potent strengths is bridging theory and application. For example, solving a system of equations becomes more meanolinidisciplinary when applied to budgeting or physical motion problems.
This not only reinforces understanding but also illustrates algebra’s relevance, transforming abstract exercises into tangible tools.
Essential Answers: From Quadratic Equations to Functions
The curriculum confronts learners with a spectrum of algebraic challenges—from foundational linear equations to advanced polynomial and rational functions. Answering these correctly demands both procedural fluency and conceptual insight.
Solving Linear and Quadratic Equations with Confidence
Linear equations form the building block. Students learn to isolate variables through inverse operations, but mastery extends to recognizing need for factoring, completing the square, or the quadratic formula.
For example: - A problem like \(2x + 3 = 7\) demands direct linear solving: subtract 3, divide by 2. - A quadratic such as \(x^2 - 5x + 6 = 0\) reveals deeper strategy: factoring into \((x-2)(x-3) = 0\), yielding \(x = 2\) or \(x = 3\). Why the Quadratic Formula Matters Although factoring isn’t always possible, the formula \(x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\) remains indispensable.
It not only solves any quadratic but also clarifies how discriminant values determine solution nature—real, repeated, or imaginary. As instructional guides emphasize, “Understanding why the formula works empowers students beyond memorization.”
Mastering Functions: Input, Output, and Relationships
Function understanding underpins advanced algebra. Students dissect input-output dynamics, analyze slopes and y-intercepts, and interpret linear and nonlinear models.
Key skills include: - Identifying function notation: \(f(x)\), \(y = mx + b\), versus relation ambiguity. - Recognizing transformations: shifts, stretches, and reflections in graphs. - Translating word problems into functional forms (e.g., “a car travels 60 mph” → \(d = 60t\)).
Applications abound in physics, economics, and technology—graphing functions becomes less about parsing tables and more about predicting trends and solving optimization challenges.
Real-World Application: Algebra as Decision-Making Tool
Perhaps Apex Algebra 1’s most transformative strength lies in applying algebra to authentic scenarios. Consider a student tasked with comparing phone plans: linear cost equations help determine break-even points, while exponential models illustrate variable-rate pricing over time. Similarly, calculating compound interest requires understanding growth formulas, while projectile motion relies on quadratic equations.
These applications bridge classroom learning and daily life, proving algebra’s utility far beyond exams.
The Cognitive Benefits of Pursuing Algebraic Rigor
Engaging deeply with Apex Algebra

![Binoculars Are Or Is pro: [8+] Apex Learning Answers Algebra 1 Semester ...](https://i3.ytimg.com/vi/bsU_04tcDCs/hqdefault.jpg)
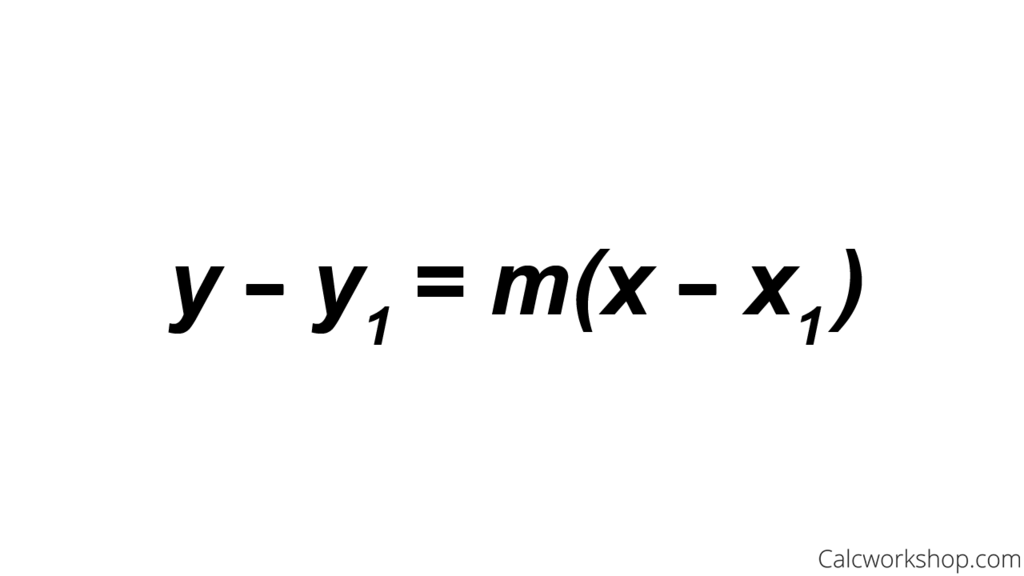
Related Post

Los Angeles Chargers’ Depth Chart Revealed: Where Every Backup Plays a Strategic Role

Ohio U: Discover Your Future Through Strategic Course Offerings in a Modern University System

Unlock Free Fire’s Epic Potential with YouTube Descriptions That Skyrocket Views

This Crazy Invention Could Replace Elevators Forever — Elisha Otis and the Skyscraper’s Hidden Lifeline

