The Crucial Blueprint: Mastering Holt Geometry Chapter 11 Section Quiz Lessons 11.1 through 11.3 Answers

Understanding how to decode and master the core content of Holt’s Geometry Chapter 11—particularly Quizzes Lessons 11.1 through 11.3—represents a transformative step in developing geometric proficiency. These sections blend foundational concepts with targeted assessment, offering a structured pathway to internalize key ideas. Careful analysis of the quiz lessons reveals not just facts, but the logic underpinning geometric reasoning—patterns, relationships, and valid inferences—that define mastery in Euclidean geometry.

This article dives deep into the essential content, presenting the essential answers and explanations behind Quizzes Lessons 11.1 to 11.3, ensuring learners build solid, test-ready knowledge.

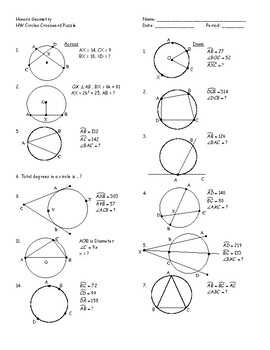
Quiz Lesson 11.1 sets the stage with fundamental concepts central to angle classification and line relationships. A primary focus is identifying types of angles—acute, obtuse, right—and understanding their implications in geometric proofs and constructions.

The lesson emphasizes that the sum of angles in a triangle is always 180°, a critical principle underlying advanced problem-solving. Equally important is recognizing complementary and supplementary angles, whose additive properties—180° and 90° respectively—form the basis for solving complex angle relationships. Quizzically, students are often tested on visually interpreting diagrams and recalling key angle sum formulas, making precision in identifying these relationships a benchmark of understanding.

Moving to Quiz Lesson 11.2, the emphasis shifts to parallel lines and transversals, a cornerstone topic in geometry that bridges multiple concepts.

Here, the concept of corresponding, alternate interior, and consecutive interior angles is explored through multiple-choice and diagram-based questions. The lesson stresses how parallel lines offset by a transversal produce predictable angle pair relationships—relationships that are not only visual but logically consistent. Students must distinguish by earned reasoning which angle pairs are equal and which are supplementary or complementary.

This section trains learners to translate visual patterns into algebraic expressions, a skill indispensable for proof-writing and coordinate geometry applications.

Quiz Lesson 11.3 advances into algebraic integration within geometric reasoning. Here, students apply variables to represent unknown angles and lengths, linking algebraic equations to geometric constraints. The quiz components often present systems of equations derived from angle sum rules or parallel line theorems, requiring solvers to balance variables and constants within geometric frameworks.

This fusion of algebra and geometry transforms abstract numbers into meaningful spatial relationships—proving the interconnectedness that defines advanced geometry. Mastery depends on recognizing how equations model real-world geometric scenarios and verifying solutions through angle measures or segment comparisons.

Deciphering Angle Properties and Their Quizzical Significance

At the heart of these quizzes lies a rigorous examination of angle properties rooted in Euclid’s postulates. Students encounter repeated scenarios: - Determining whether an angle is acute (less than 90°), right (exactly 90°), or obtuse (greater than 90°) based on diagram cues.

- Applying angle addition theorems, such as the sum of angles in polygons, to deduce unknown measures. - Recognizing vertical angles—always congruent—even in irregular diagrams. Each question tests not only recall but logical deduction: identifying which rule or property applies in a given configuration.

For instance, a triangle with two angles marked at 65° each prompts a quick conclusion: the third must be 50° (since 180° − 65° − 65° = 50°), a straightforward yet foundational computational skill reinforced through repeated quiz practice.

A common misconception addressed in these lessons involves mistaking supplementary angles (summing to 180°) for complementary angles (summing to 90°). Quizzes frequently test this distinction with diagrams lacking obvious pairings, requiring students to visually scan and mentally test combinations before marking answers.

This attention to detail prevents cascading errors in multi-step problems. Furthermore, quadrant relationships in coordinate geometry and angle measures derived from radian-transformed degrees are subtly reinforced, preparing learners for advanced spatial calculations.

Transversal Behavior and Its Role in Parallel Line Proofs

Quiz Lesson 11.2 elevates precision by focusing on transversals cutting across parallel lines—a recurring theme in geometry's most powerful theorems. The lessons reveal that consistent angle pairs emerge regardless of the transversal’s slope or orientation.

Corresponding angles remain equal, alternate interior angles match, and consecutive interior angles combine to 180°, forming the bedrock of parallel line proofs. Multiple-choice questions test this via visual identification: “Which pairs are congruent when a transversal crosses parallel lines?” requires students to move beyond memorization into applied logic. Real-world applications, such as determining hidden angles in road intersections or architectural blueprints, stem from this concept.

Each quiz reinforces that consistency in angle relationships across parallel systems is not accidental—it reflects inherent geometric order, a principle repeatedly