Unlocking Bond Duration: The Precision Measure That Shapes Fixed Income Investment Strategy
Unlocking Bond Duration: The Precision Measure That Shapes Fixed Income Investment Strategy
When managing fixed income portfolios, understanding bond duration is not just academic—it’s the cornerstone of effective risk management and return optimization. Defined as the weighted average time until a bond’s cash flows are received, duration quantifies how sensitive a bond’s price is to fluctuations in interest rates. At a glance, it offers a single number that encapsulates interest rate risk, but its implications run far deeper, influencing portfolio allocation, yield curve positioning, and strategic hedging decisions.
Bond duration, in essence, translates the timing of cash flows—principal repayment and coupon payments—into a metric that predicts percentage price movement for a given change in yields. “Duration is the single most powerful tool investors have to measure and manage interest rate risk,” aptly summarizes fixed income expert Dr. Emily Tran.
“It bridges the gap between theoretical yield and real-world price volatility.” Unlike simple maturity dates, which only indicate time to repayment, duration accounts for both timing and magnitude of cash flows, delivering a dynamic sensitivity measure.
There are two primary forms of duration critical to portfolio construction: Macaulay duration and modifications duration.
Macaulay Duration
measures the weighted average time until a bond’s cash flows are received, expressed in years.This metric reveals how long it takes for an investor to recoup their original investment from incoming coupons and principal. For example, a 10-year bond with consistent semiannual coupons might have a Macaulay duration of approximately 7.7 years—reflecting that nearly two-thirds of the bond’s lifetime occurs before maturity. Investors use this to evaluate the effective “expense” of time in holding a bond, especially in low-yield environments where even small price swings can erode capital.
Closely related but more action-oriented is
Modifications Duration
, which adjusts Macaulay duration by dividing it by one plus yield divided by coupon frequency. This produces a measure of price elasticity: for every 100 basis point (bp) change in yield, a bond’s price typically moves roughly by its modifications duration in percentage points. A 5-year bond with a maturity yield of 3.5% and semiannual coupons might have a modifications duration of 5.0; this implies a 10 bp yield rise would reduce its price by approximately 50 points.This conversion is indispensable for scenario analysis and hedging strategies.
Duration’s practical power is evident in portfolio construction and risk mitigation. Portfolio managers use duration as a control tool: a zero-duration portfolio is fully protected from interest rate moves, as price appreciation and loss offset one another.
A duration of 5 years indicates that for every 1% rise in yields, the portfolio declines by 5% in value, and vice versa. This linear approximation holds for small shifts but requires caution at larger rate changes, where convexity—a second-order measure—becomes essential. “While duration is a first-order approximation,” notes financial analyst James Reed, “convexity captures how duration itself changes with volatility, offering a more accurate preview of large yield swings.” Real-world application demands understanding duration in context.
Yield Curve Sensitivity
reveals how bonds at different maturities respond differently to yield shifts. Short-duration bonds—for instance, 1- to 3-year treasuries—exhibit low duration and minimal interest rate exposure, making them favored during rate-hike cycles. Conversely, long-duration bonds—say, 10- or 30-year issues—suffer more price volatility but offer enhanced capital appreciation potential when rates fall.Investors seeking inflation-linked returns often employ duration gradient strategies, layering bonds across the curve to balance risk and yield.
Calculating duration involves meticulous weighting of cash flows, a process requiring precise assumptions about future payments and reinvestment rates. \「Diameter of cash flow timing is where duration’s accuracy hinges,” explains Diane Cho, a senior fixed income strategist.
“Even a single unexpected coupon or early redemption can skew results if not properly modeled.” Common formulas include: - Macaulay duration: T = Σ (t × CFt × PVF(r,t)) / P - Modifications duration: D = Macaulay duration / (1 + y/n) Where CFt = cash flow at time t, y = yield, n = coupon frequency, r = spot rate, PVF = present value factor. Portfolio-level duration is slightly complicated by bond clustering and liquidity. Diversifying across issuers, sectors, and geographies maintains a consistent duration profile, but non-standard instruments—like callable or puttable bonds—distort cash flow patterns, necessitating convexity adjustments.
In practice, bond duration serves as both compass and shield. It enables investors to anticipate rate impacts, align holdings with risk tolerance, and fine-tune portfolios amid shifting monetary policies. “Bond duration isn’t just a number—it’s


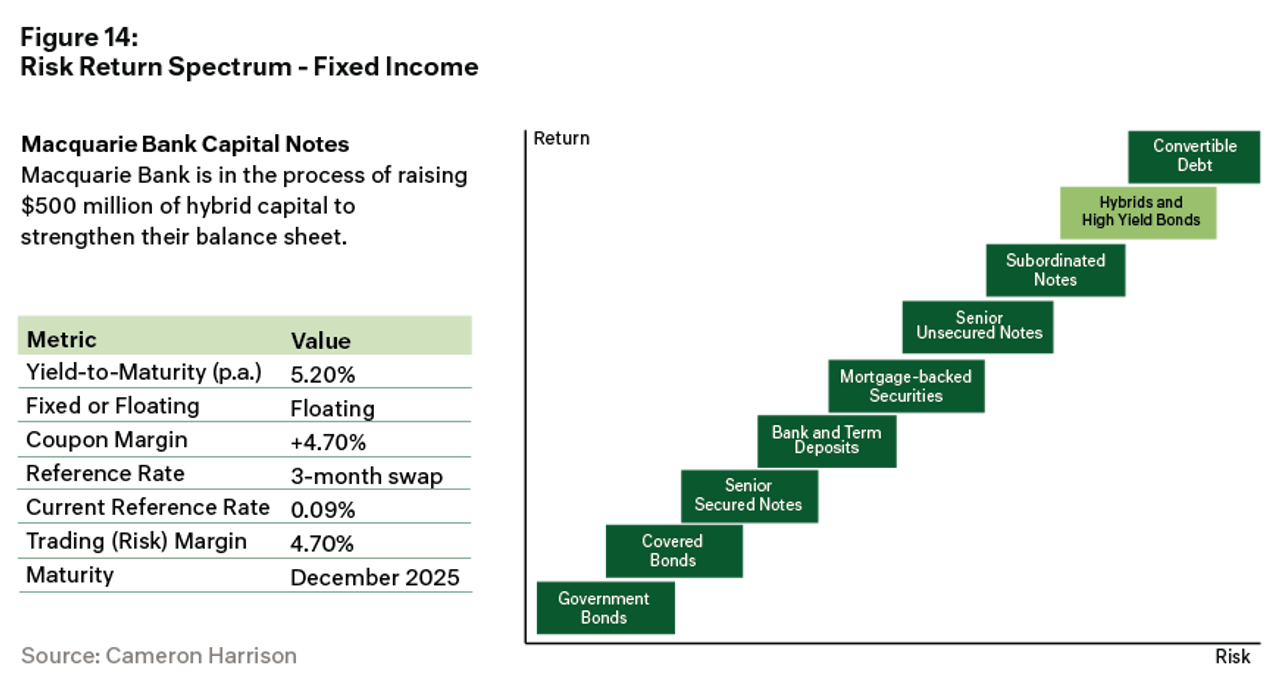
Related Post
Is Alamogordo, NM a Safe Place to Live? Decoding Crime Rates and Community Security
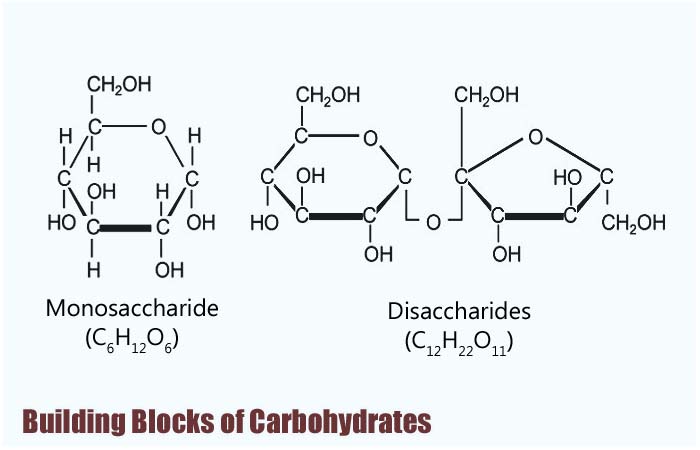
What Are the Monomers of Carbohydrates? Decoding the Building Blocks of Life’s Most Abundant Molecules

Nephew Tommie: Where Resilience, Legacy, and Mentorship Collide in American Life

Rockford Police Scanner Reveals Real-Time Crime Snapshots of a Midwestern City

