Unlocking Right Triangles: How SecTrigonometry Transforms Angle Analysis
Unlocking Right Triangles: How SecTrigonometry Transforms Angle Analysis
In the intricate dance of geometry and angle measurement, SecTrigonometry stands as a pivotal tool—transforming abstract triangles into quantifiable, actionable data. By leveraging the secant function within secant trigonometric principles, professionals across engineering, architecture, and physics unlock precise relationships between sides and angles in right triangles, enabling everything from structural stability assessments to complex motion analysis. This approach, grounded in SecTrigonometry, turns abstract concepts into tangible solutions, proving indispensable in fields where accuracy defines success.
At its core, secant trigonometry operates on the unit circle and right triangle relationships, where sec(θ) = 1/cos(θ).
Defined as the ratio of the hypotenuse to the adjacent side (sec θ = hypotenuse / adjacent), it complements sine, cosine, and tangent by focusing on exterior angles in right triangles and extending their utility into real-world design and navigation. Unlike sine, which centers on opposite-to-adjacent ratios, secant reveals relationships tied to complements—offering a dual lens critical for deep spatial understanding.
Core Principles of SecTrigonometry: Beyond the Basics
SecTrigonometry draws from fundamental trigonometric foundations but introduces a unique perspective rooted in the secant function. Unlike right triangle nomenclature that often emphasizes opposite, adjacent, or hypotenuse components directly, secant highlights the hypotenuse’s role relative to adjacent sides—a framing particularly useful in applications involving external angles or extended projections.
For any angle θ in a right triangle:
- Adjacent-side ratio: Adjacent / Hypotenuse = cos θ → Complementary to cosine, sec θ directly captures the hypotenuse-to-adjacent ratio.
- Right triangle definition: sec θ = hypotenuse / adjacent = 1 / cos θ
- Domain and range: Defined for cos θ ≠ 0, sec θ exists for all θ excluding odd multiples of π/2, covering infinite real values across asymptotic ranges
This mathematical structure positions secant not as a replacement, but as a complementary lens—especially valuable when analyzing angles beyond 90° or working with non-obvious geometric relationships. “Secant trigonometry fills a critical niche,” explains Dr. Lena Marquez, applied mathematician at Geotech Solutions.
“While sine and cosine excel at describing immediate triangle dynamics, secant lets engineers map load paths, predict structural deflections, and model trajectory shifts with greater precision.”
Applications: From Structures to Space Exploration
SecTrigonometry’s practical utility spans disciplines where spatial accuracy is non-negotiable. In civil engineering, secant models help calculate력을 across diagonal beams or inclined supports, transforming ambiguous angles into measurable stress vectors. For example, in bridge design, sec(θ) enables engineers to determine the exact tension forces acting along the hypotenuse of a truss when external loads create non-right-angled joist intersections.
Astronomy and satellite navigation rely on secant trigonometry to resolve celestial trajectories.
When tracking a spacecraft’s elliptical path, modern orbit codes use sec θ to relate positional vectors to angular deviations, ensuring accurate trajectory corrections. “The secant function decodes orbital eccentricity more cleanly than basic cosine ratios,” says astrophysicist James Tran. “It naturally encodes how solar gravitational pull shifts from perpendicular to tangential—information vital for data-driven mission planning.”
Surveying and geodesy use secant relationships to measure vast distances across non-flat terrain.
By analyzing angles from vantage points spanning hills or valleys, professionals apply sec(θ) to compute elevation changes and horizontal shifts with millimeter-level accuracy, even when direct line-of-sight is obstructed. “In mountainous regions, secant trigonometry bridges observation gaps—transforming scattered angular data into coherent topographic maps,” notes geospatial analyst Sofia Chen.
SecTrigonometric Identities and Advanced Problem Solving
Beyond direct triangle analysis, secant interacts with other trigonometric functions through well-established identities that enhance problem-solving versatility. Key among them:
1.
Pythagorean Identity: sec² θ = 1 + tan² θ
Reversing the cosine identity, sec² θ = 1 / cos² θ and 1 + tan² θ = sec² θ—this equivalence enables seamless conversion between forms when simplifying complex expressions.
2. Complementary Angle Relationships: sec(90° − θ) = sec θ
3. Secant with the Law of Cosines: For non-right triangles, sec A = (b² + c² − a²) / (4Δ / a), where Δ is triangle area—showcasing secant’s role in advanced geometric modeling.
In practical problem solving, these identities empower practitioners to reframe challenges.
When dealing with angles where standard cosine approaches are inefficient or ambiguous, switching to secant often simplifies derivations. For instance, resolving forces in a mechanical linkage may require opposite-side ratios—secant’s hypotenuse focus, though counterintuitive, directly supports inverse trigonometric inversions needed for precise reconstruction of vector components.
Limitations and Best Practices in Securing Accuracy
While powerful, secant trigonometry demands cautious application. Its undefined nature at θ = 90°(π/2)k (where cos θ = 0) requires vigilance—misidentifying angle positions can yield infinite or undefined results, compromising calculations.
“Secant isn’t a silver bullet,” warns Dr. Marquez. “Always verify solutions within context—especially when angles span discontinuities.”
Best practices include:
- Confirming angle placement relative to the right triangle’s axis—secant depends on ray orientation.
- Validating secant inputs against complementary trigonometric identities to cross-check results.
- Using secant in tandem with sine and cosine when multi-angle relationships demand balanced analysis.
Professional engineers and surveyors integrate secant within layered analytical frameworks—never in isolation.
“It’s not about replacing other functions,” Tran remarks. “It’s about expanding your toolkit, ensuring you capture every geometric nuance.”
As computational precision increases, secant trigonometry’s role evolves—no longer just a classroom concept but a real-world engine driving innovation in design, measurement, and exploration. By mastering its logic, users transform abstract triangles into dynamic models, unlocking deeper insight with every calculation.
SecTrigonometry exemplifies how mathematical elegance meets practical power.
Its secant function bridges theoretical geometry and applied engineering, offering a refined lens through which angles become vectors of data. In a world where precision defines progress, SecTrigonometry isn’t just a tool—it’s the language that turns triangles into truth.



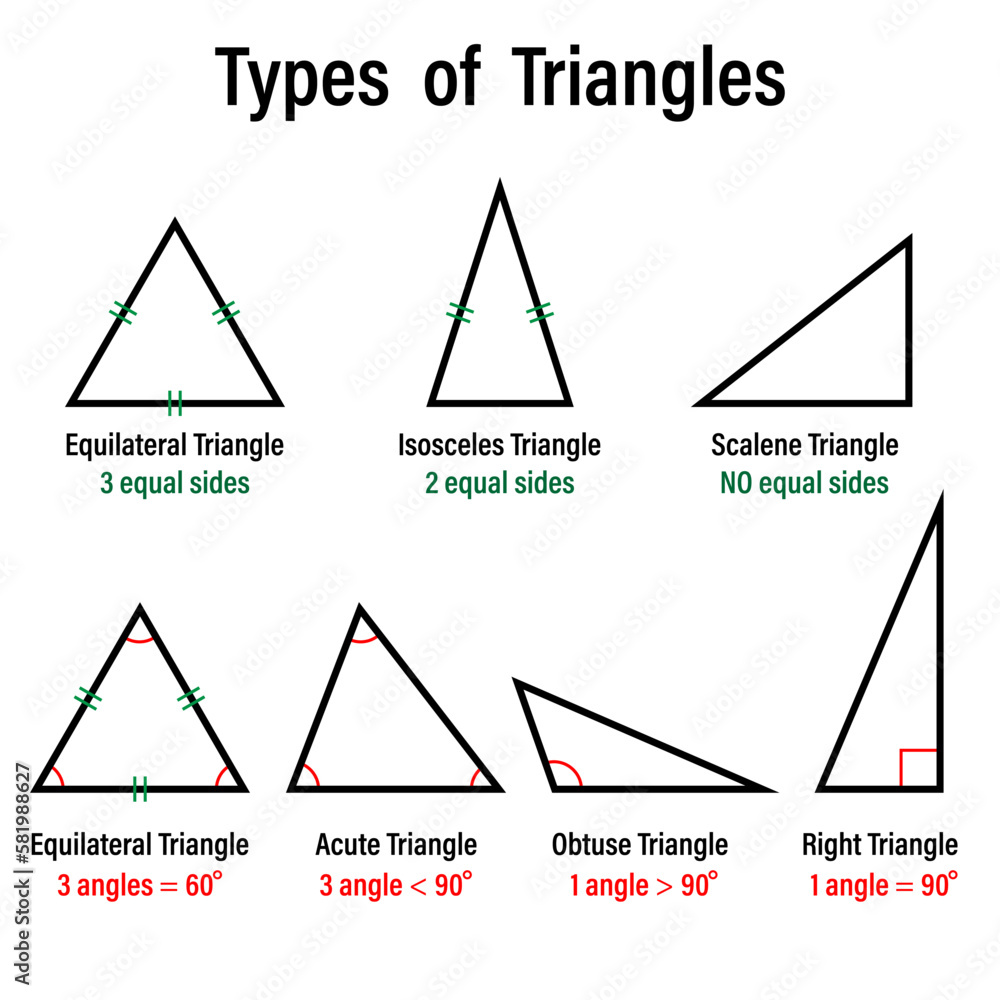
Related Post

Pseicerundolose vs. Schwartzman: A Definitive Clash of Mathematical Minds

From Omnibus to Net Billionaire: Exploding with a Net Worth of Over $100 Million

Unlock Algebraic Success: Mastering Avancemos 1 with the Teacher Edition
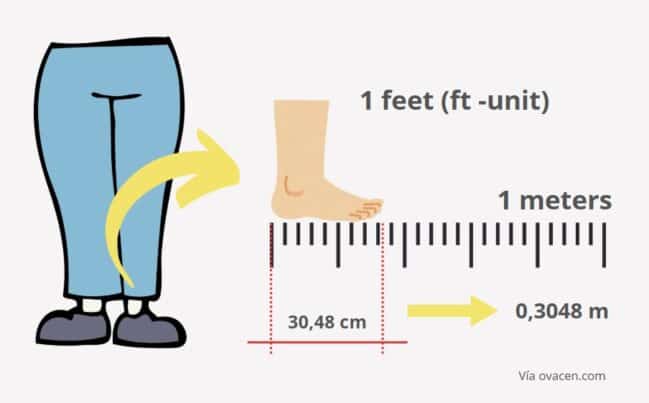
35 Meters to Feet: Decoding One of the World’s Most Used Length Conversions

